輕鬆了解Entropy(熵): 分類模型中評估變數的好幫手

前言

好久沒寫數據專題了，最近看完資料科學神書「Data Science for Business」，覺得裡面內容淺顯易懂值得整理分享，預計將會整理成幾篇專題，除了當作我個人的筆記外，也分享給需要人囉！

為什麼我們需要Entropy(熵)

建立模型的過程中，有一個大哉問是: 變數很多，該如何選擇?  想像大海撈針的感覺，如果能夠正確而有效的選擇變數，不僅效能會提升，且模型正確度也會有效增加。舉實際案例來說，假設我們要解決「到底什麼樣的人容易倒帳? 」 那我們可以將問題簡化如下:

1. 目標變數:  將過往資料分成兩種目標，實際有倒帳的人、沒倒帳的人 

2. 選擇變數:  各種質化、量化標準。為了讓視覺化方便，我們分成以下有趣的特徵，這些不同特徵可以帶進平常所看的變數，像是是否為年輕人、居住狀況、男女、婚姻性別....等等。

(1) 頭型: 方形、圓形

(2) 身體: 長方形、橢圓形

(3) 顏色: 灰色、白色

資料來源: Data Science for Business

一個理想狀態是，假設所有倒帳的人，我們觀察到這些人都是橢圓形身體，那我們就知道「橢圓形身體」是推測是否倒帳的重要因子，也就是「是否為橢圓形身體」這個特徵可以將資料分成兩組，是橢圓形都是倒帳的人、不是橢圓形身體都是沒有倒帳的人，這樣分出來的兩個群組都是非常純粹的(pure)。

現實與理想的分群差距

但現實生活中怎麼可能有這麼好的事情?  比較常見的情況是，橢圓型身體區分兩組，兩組裡面都還是有倒帳、不倒帳的人，也就是並非純粹的群組。也有可能橢圓形身體都是倒帳的人，但是非橢圓身體的人有倒帳和沒倒帳混合，這樣一樣沒辦法取得純粹的分群。更有可能這個變數只針對某個資料節點可以得到純粹的分群，但並沒有辦法把整個母體分的很純粹，這樣可能很難挑變數了。

Entropy的計算與背後含意

Entropy(熵)就是發明來解決這個問題的，我們用Entropy(熵)來評估到底這個變數有多純粹，複雜的數學公式如下:

entropy= -p1 * log(p1) - p2*log(p2)-....

舉例來說，假設一個分群組中10人中有7人倒帳、3人沒倒帳，則entropy的算法為

entropy= -(7/10)* log(7/10) +(3/10)*log(3/10)=0.88

數字0.88乍看之下無法比較，0.88到底純不純粹阿?  但若我們拿出Entropy分布圖，就可以稍微了解背後含意，假設倒帳的標示是(+)、沒倒帳的標示是(-)，entropy分布就變成一個倒過來的U型，假設分群中全部都是沒倒帳的人，那entropy算起來是0。但當樣本一半一半，entropy就會變為最大的1，也代表達到最混亂的狀態; 隨著倒帳人比例增加，entropy慢慢下降，最後全部都是倒帳的人，樣本entropy又回到0。Entropy有點像是觀察樣本中兩個類別的比例，但是透過LOG函數把亂度這件事標準化在0~1之間。

從Entropy到Information Gain(IG)

光是算出Entropy還不夠，對於評估變數來說，Entropy越大，只告訴我們這個變數在「單一」個分群裡有多不純粹，問題是一個分類數模型有「多個」分群阿!  所以這時候需要Information Gain(IG)出場。 IG看的分群之下，當新資訊加進來時，entropy(也就是混亂程度)究竟可以下降多少。

IG的公式更加直覺，由於要判斷母體分成子集後下降亂度多少，所以用母體的entropy減去各子集的entropy，並且考慮各子集的大小，給予不同權重。

例如下圖這個例子，在母體時星星和月亮混雜，entropy亂度高達0.99! 這也不令人意外，因為這個群體裏有7個星星6個月亮，用肉眼看就大概知道不是分的很「乾淨」的群體。但當往下分子集時，子集1和子集2的的亂度較母體下降，尤其子集1，可以區分到只剩下4/5都是星星。IG的數值0反映當我們從母體切分到子集時，混亂下降的程度，若IG越高，代表切分得越乾淨、混亂下降越多。

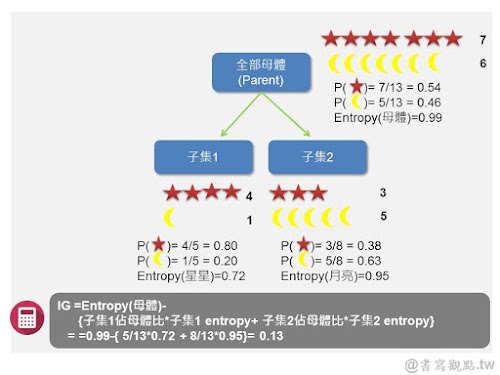Information Gain算法說明

IG可以說是一個綜合考量的亂度下降指標，因為光只有一個子集區分的乾淨並不代表整體亂度下降，與其一個子集區分非常乾淨而其他子集混亂，還不如所有子集都區分相對乾淨，亂度下降程度會更高，這也是單單衡量entropy無法做到的地方。

Entropy、IG在決策樹模型中的運用

Entropy與IG是在做決策樹時判斷的基本依據，若使用現行統計軟體功能，自動計算Entropy與IG進行分支，我們則不需要自行計算，但透過了解分支原理仍有助於幫助我們確認模型正確性，並且在需要做決策樹自行剪枝時可以手動計算。

除此之外，Entropy也是可以評估隨機森林中變數重要性的好幫手(相關文章: 請參閱部落格的另一篇隨機森林底層概念)，於隨機森林中，若我們想知道到底哪個變數是最重要的? 我們可以分別計算每個變數於各個子模型中的information gain並加總，來評估該變數於模型中減降了多少亂度。

參考資料與延伸閱讀

1. Data Science for Business(中譯本: 資料科學的商業應用)

將模型觀念講解非常清楚的數據神書，之後在部落格也會多分享關於這本書的精彩內容，敬請期待。

2. 決策樹探討文章

網路上關於entropy的中文解釋文章不多，這篇從決策樹開始，寫的相對淺顯易懂，可以參考看看。